Cost methods
The ETM defines six main cost groups, consisting of various subgroups. These subgroups are the sum of individual technologies and some additional modules. A detailed breakdown of all groups, subgroups and modules and can be found in the data export. A detailed overview of the scope per subgroup can be found in the Overview of costs per sector.
Main cost groups
The yearly costs of a scenario in the ETM is built up from all technologies, carriers, and CO2 costs in a scenario. Important: Group 1-4 consists of the CAPEX and OPEX and exclude fuels and CCUS costs. Group 5 includes all the fuel costs and group 6 all the CCUS and CO2 costs.
- Buildings and installations: Building and installation-related costs (CAPEX + OPEX) of sectors. Subgroups:
- Households
- Buildings
- Transport
- Industry
- Agriculture
- Energy Production: Installation-related costs (CAPEX + OPEX) of the energy production sector. Subgroups:
- Power plants
- CHP plants (including the industrial steam network)
- Heat plants
- Dedicated hydrogen production
- Biomass treatment
- Other intallations (synthetic kerosine, regasification of lng, and energy compressors for network gas)
- Infrastructure: CAPEX + OPEX of the energy infrastructure. Subgroups:
- Natural gas (includes gas network for natural gas and green gas and import infrastructure costs of LNG)
- Heat (network costs)
- Hydrogen carriers (includes hydrogen network and import infrastructure costs of liquid hydrogen and LOHC)
- Electricity (network costs)
- Ammonia (import infrastructure costs of ammonia)
- Oil (import infrastructure costs of diesel)
- Storage and conversion: Installation-related costs (CAPEX + OPEX). All G2P is associated with means of 'Energy production'. Subgroups:
- Power-to-power (p2p)
- Power-to-gas (p2g)
- Power-to-heat (p2h)
- Storage (of hydrogen and heat)
Energy carriers and import: All net primary demand of energy carriers.
Cost of carrier = (extraction + import - export) * price of carrierFor export the ETM charges the costs of the primary carrier that is needed for that export. The export of electricity and transit of oil is cost neutral and independent of the market price. A country does not "earn" money from processing oil. And for electricity the ETM deducts the costs of the primary carriers needed to produce that electricity.
Carbon capture, utilisation and storage (CCUS): CAPEX + OPEX of all CCUS technologies, including CO2 costs.
CAPEX and OPEX
All costs of groups 1-4 consists of two variables: CAPEX or capital_expenditures_excluding_ccs and OPEX or operating_expenses_excluding_ccs. Group 6 is similar, but contains all CAPEX and OPEX of the CCUS technologies.
CAPEX
Capital expenditures are major investments that are designed to be used for many years. The yearly costs for these investments are based on the total investment over lifetime, WACC and plant lifetime. CCUS and fuel costs are not in the CAPEX and OPEX of group 1-4.

Additional definitions:
- Investment over lifetime = total initial investment + decommissioning costs
- WACC = Weighted average cost of capital
- Construction time = the time it takes to construct a typical plant of this type
- Technical lifetime = the average amount of time that a plant operates
OPEX
Operating expenses include Operation and Maintenance (O&M) costs, without CCS. O&M costs can have both a variable and a fixed part.
- Variable O&M costs are costs that depend on the number of full load hours of the plant, for additional cleaning and service costs. Note that this excludes fuel costs, since these are allocated to an individual category.
- The fixed part are the costs that are made yearly, independent of whether the plant is used or not. Fixed O&M Costs are specified per year and found directly from research. This means that Fixed O&M Costs have no calculations associated with them.
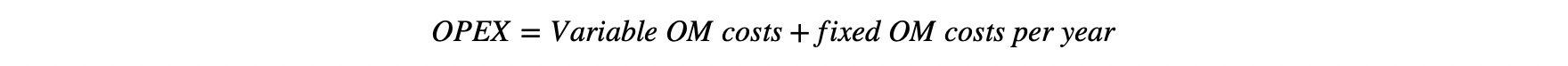
Additional definitions:
- Full load hours = the typical yearly full load hours of a plant of this type, this is calculated in the scenario.
- Variable Operation & Maintenance Costs per Full load hour = the normal costs for operating and maintaining the plant for one full load hour, this is researched per technology, see: ETDataset source analysis
Fuel costs
These costs are specified in the category "carriers". This includes all raw fuel costs. So taxes and profit margins are not taken into account.
Changing costs in a scenario
All the costs of technologies and datasets (or regions) are researched in advance. Technologies have the same starting assumptions for all regions. Carrier costs can be different per region. When making a scenario, many of these assumptions can be changed in the costs section of the ETM.